Class 10 Maths Chapter 6 Triangles Questions

 📝 Class 10 Maths Chapter 6 Triangles Questions

Multiple Choice Questions

1. Two figures having the same shape but not necessarily the same size are called similar figures.

(a) True

(b) False

(c) Cannot say

(d) Partially true/false

Ans: (a)

2. Two triangles are similar. If their corresponding angles are proportional. 

(a)True

(b) False

(C) Cannot say

Ans: (b)

3. All ........... triangles are similar.

(a) equilateral triangle

(b) right triangle

(c) scalene triangle

(d) None of this

Ans: (a)

4. Two triangles are similar. If their corresponding sides are..........

(a) equal

(b) proportional

(c) right angle

(d) None of the above

Ans: (b)

5. If in fig, O is the point of intersection of two chords AB and CD such that OB = OD, the `triangleOAC` and `triangleODB` are

(a) equilateral but not similar

(b) isosceles but not similar

(c) equilateral and silimar 

(d) isosceles and similar

Ans: (d)

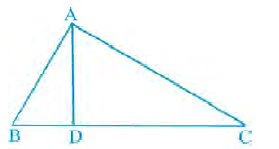
6. In Fig., `angleBAC = 90°` and `AD ⊥ BC`. Then,

(a) `BD.CD = BC^2` 

(b) `AB.AC = BC^2`

(c) `BD.CD = AD^2`

(d) `AB.AC = AD^2` 

Ans: (c)

7. The lengths of the diagonals of a rhombus are 16 cm and 12 cm. Then, the length of the side of the rhombus is 

(a) 9 cm 

(b) 10 cm 

(c) 8 cm 

(d) 20 cm  

Ans: (b)

8. If in two traingles `triangleABC` and `trianglePQR`,

`frac{AB}{QR}` `= frac{BC}{PR}` `=frac{CA}{PQ}`

(a) `trianglePQR` ~ `triangle CAB`

(b) `trianglePQR` ~ `triangle ABC`

(c) `triangleCBA` ~ `trianglePQR`

(d) `triangleBCA` ~ `trianglePQR`

Ans: (a)

9. If in two triangles `triangleDEF` and `trianglePQR`,

`angleD = angleQ` and `angleR = angleE`, then which of the following is not true?

(a) `frac{EF}{PR} = frac{DF}{PQ}`

(b) `frac{DE}{PQ} = frac{EF}{RP}`

(c) `frac{DE}{QR} = frac{DF}{PQ}`

(d) `frac{EF}{RP} = frac{DE}{QR}`

Ans: (b)

10. If `triangleABC ~ triangleEDF` and `triangleABC ≁ triangle DEF`, then which of

the following is not true

(a) `BC.EF = AC.FD`

(b) `AB.EF = AC.DE`

(c) `BC.DE = AB.EF`

(d) `BC.DE = AB.FD`

Ans: (c)

11. In Fig. two line segments `AC` and `BD` intersect each other at the point `P` such that

`PA = 6`cm, `PB = 3`cm, `PC = 2.5` cm, `PD = 5`cm, `angleAPB = 50°` and `angleCDP = 30°`, then

`anglePBA = ?`

(a) 50°

(b) 30°

(c) 60°

(d) 100°

Ans: (d)

12. In `triangleABC` and `triangleDEF`, `angleB = angleE, angleF = angleC` and AB = 3DE.

Then two triangles are

(a) congruent but not similar

(b) similar but not congruent

(c) neither congruent nor similar

(d) congruent as well as similar

Ans: (b)

13. It is given that `triangleABC ~ trianglePQR`, with `frac{BC}{QR} = 1/3`.

Then `frac{ar(trianglePRQ)}{ar(triangleBCA)}=`

(a) `9`

(b) `3`

(c)`1/3`

(d) `1/9`

Ans: (a)

14. It is given that `triangleABC ~ triangleDEF , angleA = 30°, angleC = 50°`, `AB = 5`cm

`AC = 8`cm and `DF = 7.5` cm. Then the folllowing is true:

(a) `DE = 12`cm, `angleF = 50°`

(b) `DE = 12` cm, `angleF = 100°`

(c) `EF = 12` cm, `angleD = 100°`

(d) `EF = 12` cm, `angleD = 120°`

Ans: (b)

15. If `triangleABC ~ triangleQRP, frac{ar(triangleABC)}{ar( triangleQRP)} = 9/4`

AB = 18cm and BC = 15 cm, then PR = ?

(a) 10 cm

(b) 12 cm

(c) `20/3` cm

(d) 8 cm

Ans: (a)

16. If S is the point on the side PQ of a `trianglePQR`such that PS = QS = RS, then

(a) `PR.QR = RS^2`

(b) `QS^2 + RS^2 = QR^2`

(c) `PR^2 + QR^2 = PQ^2`

(d) `PS^2 + RS^2 = PR^2`

Ans: (c)

★★★★★★

Case Studies 

1. 

Vijay is trying to find the average height of a tower near his house. He is using the properties of similar triangles.The height of Vijay’s house if 20m when Vijay’s house casts a shadow 10m long on the ground. At the same time, the tower casts a shadow 50m long on the ground and the house of Ajay casts 20m shadow on the ground.

(i). What is the height of the tower?

a) 20m

b) 50m

c) 100m

d) 200m

Ans: (c)

(ii). What will be the length of the shadow of the tower when Vijay’s house casts a shadow of 12m?

a) 75m

b) 50m

c) 45m

d) 60m

Ans: (d)

(iii). What is the height of Ajay’s house?

a) 30m

b) 40m

c) 50m

d) 20m

Ans: (b)

(iv). When the tower casts a shadow of 40m, same time what will be the length of the shadow of Ajay’s house?

a) 16m

b) 32m

c) 20m

d) 8m

Ans: (a)

(v). When the tower casts a shadow of 40m, same time what will be the length of the shadow of Vijay’s house?

a) 15m

b) 32m

c) 16m

d) 8m

Ans: (d)

2. Rohan wants to measure the distance of a pond during the visit to his native. He marks points A and B on the opposite edges of a pond as shown in the figure below. To find the distance between the points, he makes a right-angled triangle using rope connecting B with another point C are a distance of 12m, connecting C to point D at a distance of 40m from point C and the connecting D to the point A which is are a distance of 30m from D such the `angleADC=90°`.

1. Which property of geometry will be used to find the distance AC?

a) Similarity of triangles

b) Thales Theorem

c) Pythagoras Theorem

d) Area of similar triangles

Ans: (c)

2. What is the distance AC?

a) 50m

b) 12m

c) 100m

d) 70m

Ans: (a)

3. Which is the following does not form a Pythagoras triplet?

a) (7,24,25)

b) (15,8,17)

c) (5,12,13)

d) (21,20,28)

Ans: (d)

4. Find the length AB?

a) 12m

b) 38m

c) 50m

d) 100m

Ans: (b)

5. Find the length of the rope used.

a) 120m

b) 70m

c) 82m

d) 22m

Ans: (c)

3. A scale drawing of an object is the same shape at the object but a different size. The scale of a drawing is a comparison of the length used on a drawing to the length it represents. The scale is written as a ratio. The ratio of two corresponding sides in similar figures is called the scale factor

Scale factor `= `length in image / corresponding length in object

If one shape can become another using revising, then the shapes are similar. Hence, two shapes are similar when one can become the other after a resize, flip, slide or turn. In the photograph below showing the side view of a train engine. Scale factor is 1:200

This means that a length of 1 cm on the photograph above corresponds to a length of 200cm or 2 m, of the actual engine. The scale can also be written as the ratio of two lengths.

1. If the length of the model is 11cm, then the overall length of the engine in the photograph above, including the couplings (the mechanism used to connect) is:

a) 22cm

b) 220cm

c) 220m

d) 22m

Ans: (a)

2. What will affect the similarity of any two polygons?

a) They are flipped horizontally

b) They are dilated by a scale factor

c) They are translated down

d) They are not the mirror image of one another.

Ans: (d)

3. What is the actual width of the door if the width of the door in the photograph is 0.35cm?

a) 0.7m

b) 0.7cm

c) 0.07cm

d) 0.07m

Ans: (a)

4. If two similar triangles have a scale factor 5:3 which statement regarding the two triangles is true?

a) The ratio of their perimeters is 15:1

b) Their altitudes have a ratio 25:15

c) Their medians have a ratio 10:4

d) Their angle bisectors have a ratio 11:5

Ans: (b)

5. The length of AB in the given figure:

a) 8cm

b) 6cm

c) 4cm

d) 10cm

Ans: (c)