Class 10 Maths Chapter 10 Circles

 📝 Chapter 10 Circles

Circle

A circle is a collection of all points in a plane that are at a constant distance (radius) from a fixed point (centre).

Let us now examine the different situations that can arise when a circle and a line are given in a plane. Let us consider a circle and a line PQ. There can be three possibilities given in Fig.

(i) The line PQ and the circle have no common point. In this case, PQ is called a non-intersecting line with respect to the circle.

(ii) There are two common points A and B that the line PQ and the circle have. In this case, we call the line PQ a secant of the circle.

(iii) there is only one point A which is common to the line PQ and the circle. In this case, the line is called a tangent to the circle.

Secant 

A line that intersects a circle in two distinct points is called a secant to the circle. [Fig. ii]

Tangent

A tangent to a circle is a line that intersects the circle at only one point. 

Point of contact

The common point of the tangent and the circle is called the point of contact [the point A in Fig.  (iii)] and the tangent is said to touch the circle at the common point.

Tangent to a Circle

 See the positions P'Q' and P''Q'' of the secant in Fig. This also helps you to see that there cannot be more than two tangents parallel to a given secant.

The tangent to a circle is a special case of the secant when the two endpoints of its corresponding chord coincide.

Relationship between radius and tangent 

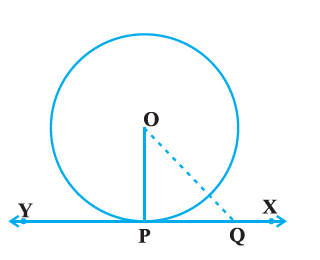
➤Theorem: The tangent at any point of a circle is perpendicular to the radius through the point of contact. 

OP ⊥ XY

Number of Tangents from a Point on a Circle

Case 1: There is no tangent to a circle passing through a point lying inside the circle.

Case 2: There is one and only one tangent to a circle passing through a point lying on the circle.

Case 3: There are exactly two tangents to a circle through a point lying outside the circle.

`T_1`and `T_2` are the points of contact of the tangents `PT_1` and `PT_2` respectively.

Length of the tangent 

The length of the segment of the tangent from the external point `P` and the point of contact with the circle is called the length of the tangent from the point `P` to the circle.

➤Theorem: The lengths of tangents drawn from an external point to a circle are equal.