Circles
1. The tangent at a point C of a circle and a diameter AB when extended intersect at P.
If `angle`PCA=110º , find `angle`CBA [see Fig. ].
3. In Fig. common tangents AB and CD to two circles intersect at E. Prove that AB = CD.
4. In Fig, tangents `PQ` and `PR` are drawn to a circle such that `angleRPQ = 30°`. A chord `RS` is drawn parallel to the tangent `PQ.` Find the `angleRQS.`
Ans:5. From a point `P`, two tangents `PA` and `PB` are drawn to a circle `C(0, r)`. If `OP = 2r`, then find `angleAPB`. What type of triangle is` APB`?
6. Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact to the centre.
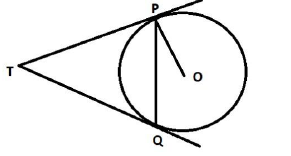
7. Two tangents `TP` and `TQ` are drawn to a circle with centre `O` from an external point `T`. Prove that `anglePTQ= 2angleOPQ`.





Very nice ques.
ReplyDeleteThanks for providing helpful question✌ ☺
ReplyDelete